如下四次隐函数,如何通过grasshopper进行绘制图形。(x^2 + y^2)^2 - 2 x (x^2 + y^2) + y^2=0
看起来你需要先“解方程”,得到 Y与 X之间的关系,例如 Y=kX+b, 这样你可以将这些关系引入 Construct Point 运算器 来建立点,有了点就可以将这些点引入 Nurbs Curve 运算器 或 Interpolate 运算器来建立曲线
1 个赞
这个方程是比较经典的心形线(Cardioid)方程,正如前面 Jessesn 所说,你要通过求解方程式找到 y 和 x 的显式关系,然后构建出一个范围内的点坐标,最后连成曲线即可,但是很显然,这个求解没那么简单。
你可以借助一些现成的数学求解平台,例如:
https://mathsolver.microsoft.com/zh/solve-problem/@9w14vfjk
我觉得可以换个思路,通过参数方程来实现,这个才是 GH 中比较对口的解决办法:
https://zh.wikipedia.org/wiki/心脏线
这里有关于 GH 中隐式函数的讨论。
https://discourse.mcneel.com/t/problem-while-writing-function/90429/7
1 个赞
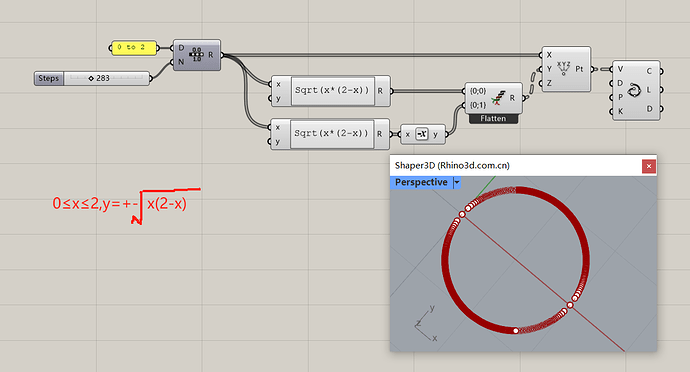
GH绘制曲线的思路
转化为y=f(x)或者x=g(y)
如果不行则选用参数方程(配合GH的极坐标)
不知道这个公示代表什么形状,有没有参数方程的情况下
可以求助大语言模型
1 个赞
可以把这个方程展开做成关于y^2的降幂排列:y^4+(2x^2-2x)y^2+x^4-2x^3=0,使用二次方程求根公式求出y^2的关于x的表达式(请注意取值范围需要>0以及根号内部的判别式>0),即可作图
1 个赞