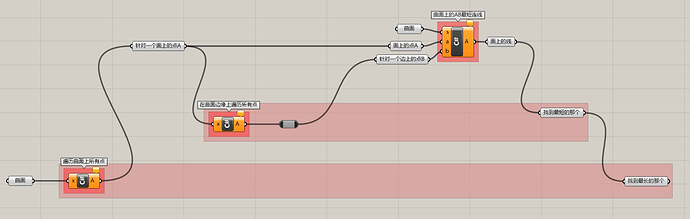
平面上任意一点都存在距该平面边界的最短连线（位于该平面上），那么GH中如何求得在所有平面上点距平面边界的最短连线中最长的连线？
请将点Pull 至曲面，然后在原来的点和Pull所得到的点之间连线，这样就会得到最短的曲线。
J神：我没有太懂你的意思，可能我的问题没有表述清楚。我是想知道，比如Rhino中有一个曲面，如何求出一条位于该曲面上的曲线，它的一个端点A在曲面上，另一个端点B在曲面的边界上，并且端点B是端点A距离曲面边界的最近点，那么在所有这种曲线中最长的那条如何计算出来。
抱歉，是我没有读懂你的意图，如果是求平面上某一点距离平面边缘的某一点的最短距离，应该是两点之间直接连线即可，两点间最短距离是通过两点的直线。
我不记得有最长曲线的方案 ，但有最短曲线的方法 SHORTEST WALK, 详情请浏览
类似 Rhino中的指令 ShortPath，
https://docs.mcneel.com/rhino/7/help/zh-cn/index.htm#commands/shortpath.htm#(null)
谢谢J神，我再琢磨琢磨。 
问题挺复杂的，应该不是最短路径这类图论算法，因为那是给已经有了图结构的数据结构设计的算法。你这个找自带电池是没戏了，直接上galapago吧，不然自己写代码费不着
谢谢鹿神的指点！
你的问题一开始是平面，后来描述为曲面，这两个问题的难度不是一个数量级。这个你得确认一下。
我现在就假设你说的是曲面
galapago应该是远远不够的，因为你的问题涉及到三重嵌套
我个人建议：放弃
能做，但是得写大量代码，甚至不一定求出最优解
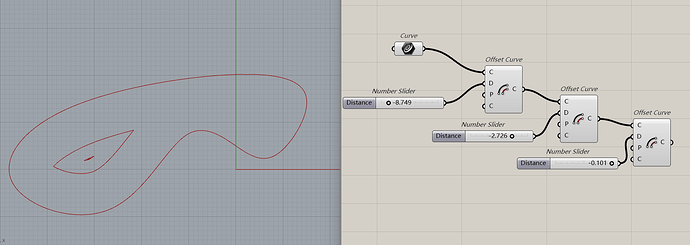
在平面上问题应该能转换成一个平面轮廓，向内偏移数值为多少是，偏移曲线退化为一个点，既然偏移数值是线性的那么我们应该可以通过二分法来找到一个可能合适的解，或者通过偏移曲线面积来得到一个足够优化的解集区域。
1 个赞
我随便列举一下其中的坑，从第三个开始
假设我们采用最简单的，两点先拉一条直线，然后pull回去，pull的GH帮助不详细，可以查看犀牛帮助
注意他的描述是顺着曲面法线
我们无法保证按照这个算法得出的曲线，再经由输入直线后，一定能获取到最短曲线
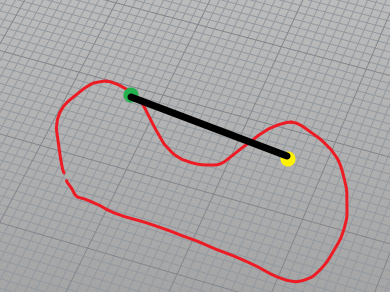
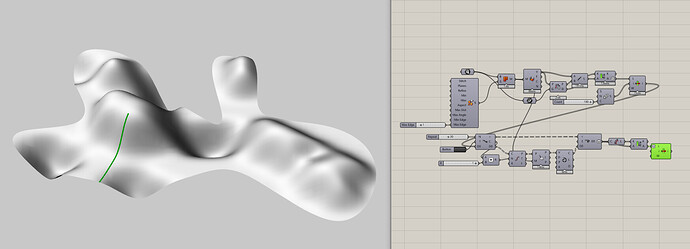
何况还有很明显的返利那就是腰子形状的曲面该如何处理。光是这一步就已经足够困难。如下图
假设你排除万难最后做出第三步了，接下来我们看第二步，也就是中间那个C#所示位置，这其实就是最典型的局部最优解问题。如下图
计算机在使用迭代/二分法/梯度下降等算法时，非常容易“短视”也就是陷入局部最优。人可以一目了然，计算机要解决这类问题可复杂多了。
这是目前人工智能领域最炙手可热的话题之一，如果有朝一日你能找到这类问题的终极解决办法，能同时获得图灵奖和诺贝尔数学奖。
最后第一步，假设你真的搞定了后面两步的算法，那么这一步你可以放心大胆使用galapago了，不过在这个情况下我相信你已经掌握人类最领先的科技了，不会再去使用GH自带的什么遗传算法。。。
还是建议放弃。没必要，也没有人要求你研究那么复杂的问题。
你的思路很不错，利用犀牛的强大几何库来辅助解决问题。
但是曲面上的曲线偏移算法属于负载非常大并且结果不稳定的算法，这个算法本来就不确定每次能获取到有效解。
他和曲面形态，曲面UV的密度等有非常大的关系。
所以我说平面上问题的转化是有希望的，曲面可能需要利用摊平等算法转化为平面再使用，摊平本身再考虑借用其他成熟算法
平面上其实都不需要offset了，因为最难的第三步直接化解了。
难点还是在曲面，摊平意味着变形，双曲面摊平一定会变形，变形后一切都白搭。
还是放弃吧
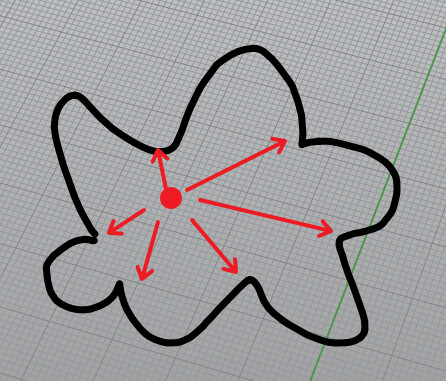
我的理解，他只是想找到曲面上距离边界最远的点而已。
你的理解部分正确，假设路径永远按照贴曲面的最小距离，在这个情况下求距离边界最远的面上的点
但是你求解的思路是错的 你用的直线最长 先找到曲面上的点，但这个点本身就不一定是曲线路径最远的
新来论坛，尽量不要去挖坟，除非
1 别人的问题没解决
2 你确定自己理解了问题并能提供正确的思路