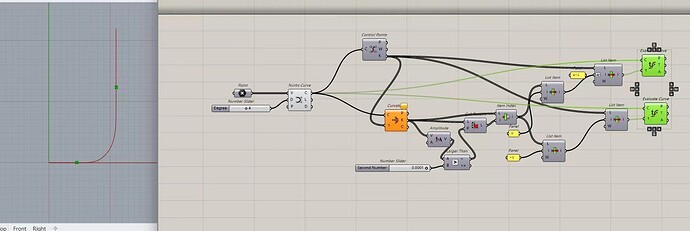
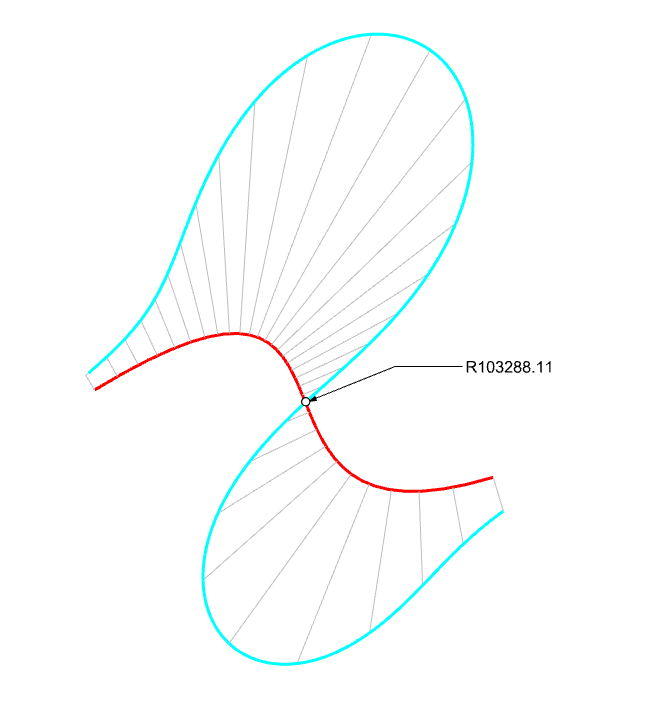
如图,我想获得曲线上曲率由零到非零的那个点,请问有什么方法?
GH有discontinuity运算器
嗯嗯,谢谢老师,俺试试
根据你发的第一个图,没发现有存在曲率=0的区域。
至于你说的曲率0到非0,其实想一下,就是直线和曲线的交界处
你可以直接打断曲线,也不需要用knot那么间接的方式,至于那个方式的具体含义,建议你问一下提供做法的人。
在我看来这个做法用来获取直线和曲线的交界点,太多此一举了。
补充+总结一下,拐点的数学定义是:
1:连续曲线中凸弧和凹弧分界点(这里的弧不是圆弧)
2:曲率从正变成负的点
3:使切线穿越曲线的点
J大给你的方法就是直接由第二点引申出来的。
而你发的第一个图,按照图面来看不存在拐点,曲率方向恒定,不明白这图的意义。
你发的第二个图,两个直线段曲率为0,也不符合拐点的定义,拐点必须针对曲线。
如果你要求的是直线变成曲线的点,可以直接炸开,但是不能用“拐点”去描述,因为这是两回事。
我在一个交流群提供过这个方法,但只是针对特定的控制点位置(前几个点共线的情况),能确定的是曲率开始不为0的点位于节点对应t值的点上,这样的结果是精确的,仅此而已。他并不是找到拐点的普适性法则,大多数曲线拐点的获得建议按照jession老师或者Deer版主的思路进行。
curvature命令可以直接找到反曲的那个点。