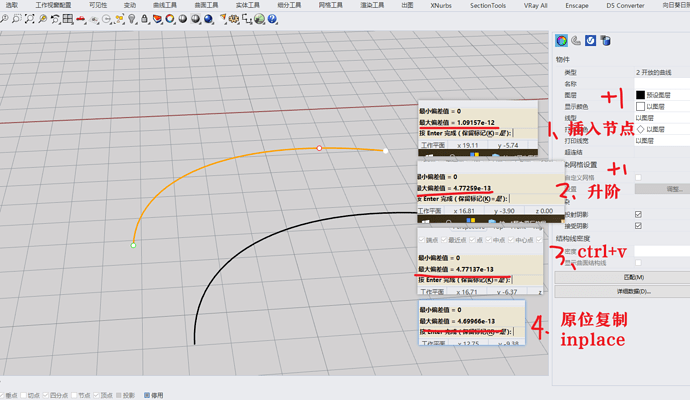
请教：就是一条曲线，分别通过1.插入节点 2.升阶 3.ctrl+c ctrl+v 4.原位复制（inplace）
得出的两条曲线都有一定误差。
插入节点和升阶有小误差，且升阶误差小于插入节点误差，这个都都还好理解。
不理解的是为什么复制粘贴甚至原位复制得到的还会有误差，为什么误差不能是绝对的0，虽然偏差结果现在是接近0，为什么不能正好是0。
现在模型单位是米，公差0.001米。
我理解你的疑惑，对于节点和升阶我就不做解释了。相信你自己也有一些概念，论坛最近关于公差和浮点数等等的讨论非常多，我也有好几条回复，J大刚才的解释看完后，如果你还有不明白，可以用论坛搜索再去搜索关键词“公差”
你最大的疑惑是，对电脑来说，不管小数点后面精确到多少位，不管公差是多少，原地复制黏贴一定是内存里面的数据的100%拷贝，为什么这个情况误差仍然不是0。
这是一个很有意思的问题。
你的假想是电脑检测这两条曲线里面的每个控制点的xyz坐标都一模一样，因为电脑内都是二进制，这4个控制点一共12个浮点数的二进制每一位都完全一样。
按照这个理解方式，这两条曲线只要用户计算偏差值，他们就应该返回0.
但实际上并不是如此，Rhino（别的软件也是）并不知道这两条曲线是用户原地拷贝的，他将这两条曲线当作两条陌生的曲线，也不会去核对他们每一个控制点的xyz是否一样。
你可以这么理解，他在做一件事情，就是用一个通用的判断偏差的工具，判断自己和自己的偏差。
我不确定底层的准确算法是什么。但我可以根据自己的理解给你提供线索：
对A进行密度比较大的采样，例如1000个点，然后这1000个点都计算到B的距离
返回给你最大偏差和最小偏差。
这个情况下你能理解节点和升阶导致的误差，就应该也能理解计算点到曲线距离导致的偏差。
这是计算机处理两个“陌生”曲线的最有可能的算法，也是最科学的算法。
我不排除有可能给这个算法加入一个前置判断（判断每个控制点的xyz坐标，判断阶数和权重）
但这样做意义不大。
谢谢解答，但是还是有点不是很清楚。所谓浮点算法我理解是不是由于计算机的限制，这些无理曲线在通过图形表达出来的时候必然会出现误差，只有类似圆这种有理曲线才能精确图形表达，不知道是不是这个意思？但是复制粘贴和原位复制难道也是逼近算法吗？复制粘贴前后的两条曲线在数学意义上还是不是同一条曲线，也就是描述该曲线的方程会不会发生变化？
描述曲线的方程不变，控制点所有数据都不变，他们是10000%相同的数据
问题出在计算偏差值的逻辑上面。
关于这个问题，请在论坛搜索“小数” 以及 “公差”
和是不是圆没有关系。公差存在于计算机内所有软件，包括你的手机里所有app
刚看到您的回复，按这个理解应该是复制前后的两条曲线其实不是同一条曲线了。刚试了下，即使是圆、圆弧，复制后的偏差也不是0。谢谢，大概理解了。
我的那么长一段解释你多半是没有耐心看。
所以你的理解还是错的。
重复第二次：复制完毕的曲线是100%一样的。
问题出在计算偏差值的逻辑上面
1：你感觉这个问题很简单，其实他不一定
2：你发现你不能理解某现象，觉得他是错误的，其实他不是
3：你认为自己的当下能力足够理解这个问题的本质，但其实暂时还没有
以上都没问题
4：你没有耐心看冗长的解释
那就完了，神仙下凡也无法拯救你 
可以这么理解吗，偏差值是一个算法工具，其采样值受计算机限制必然有误差，复制前后的曲线数据相同，产生误差的根源在于偏差值采样点的误差。
可以这么理解
我们就用一个情况做例子
在线C上找P，然后求P到C的距离，按照理论情况，这个距离应该是0
1：在线C上找一个点P，这个P本来就不一定在线上，除非你的计算机的内存容量是无穷大。你可以用无限多的位数储存一个小数。
2：这个点P再去计算到线C的距离，也不一定是0，原因同理。
之所以说不一定，是因为总有些情况，你可以用有限的位数储存一个数字，让他的计算可以没有任何误差。
注意电脑是二进制的，所以0.5是可以用有限的二进制储存，但是0.1不行，不能用十进制去理解。
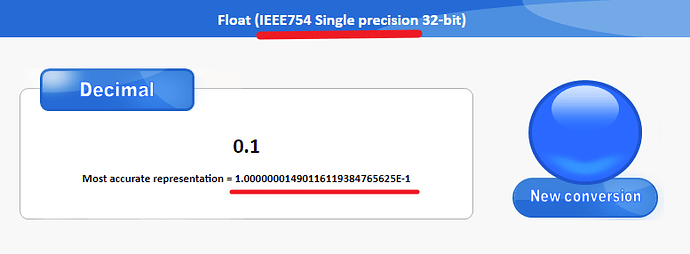
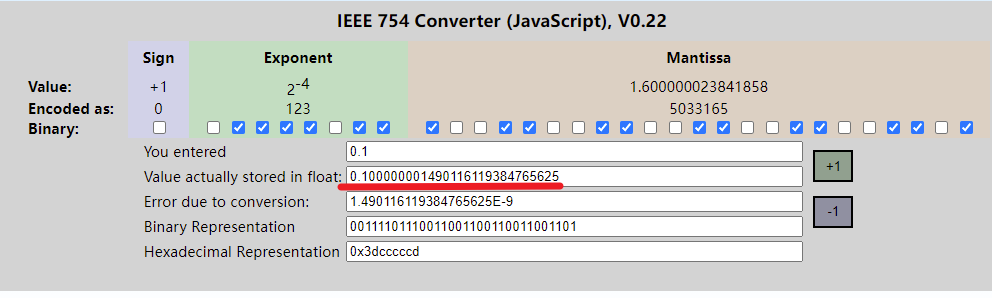
这里是两个在线二进制转化网站转化0.1的结果，精度是单精度浮点数float
因为0.1用二进制表达，是无限循环小数，但是计算机分配给浮点数的储存不可能是无限的，所以无限循环小数只能保留有限位，导致0.1在计算机的float类型里面是0.100000001490116119384765625
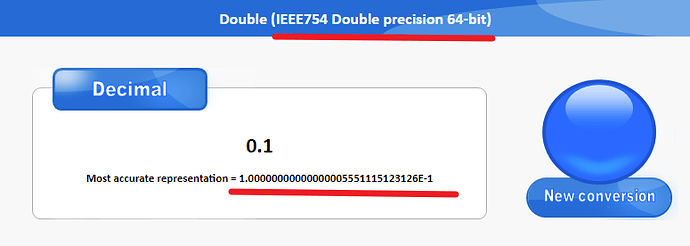
你可以使用double双精度去记录，达到更高的精度
这就是计算机处理数字的方法，加上各类复杂计算以后这个问题只会更明显。
如果是这样，我们的电脑手机都没法用了，所以计算机需要使用公差系统
假设这个数字离开0.1的距离已经小到1的-20次方那么小了，计算机会认为这两个数字是一个数字，也就是认为这个数字就是0.1
再多看看J大发的链接，巩固一下概念。
会对你将来的软件操作很有帮助
2 个赞
好的，受教了，感谢。
其实就拿我们现实世界来说，也并不存在绝对精确。比如度量衡，其实虽然有了人为规定的标准“刻度”，但这并不符合这个世界本质的尺寸单位，绝对的精确只存在于书面数字的理论计算上。
3 个赞