本人是名结构工程师,之前陆陆续续用Rhino+GH做过点小项目,不过NURBS的原理我是一直没搞明白,也一直很想搞明白,后来去自学了一下,发现其实这块是属于图形学的内容:一开始找了几本国内教材,基本NURBS这块也是讲的很少,甚至讲到B样条就不讲了;后来无意中发现 Les Piegl 和 Wayne Tiller写的 The NURBS book, 2e 这本书,并且发现一个很好的网站: CS3621 Introduction to Computing with Geometry Course Notes (mtu.edu)
:)
PS:这本书是有中文版的,名字好像就叫:非均匀有理B样条。。。在工科教材的翻译版本中,绝对算得上良心的翻译了,值得一读。
5 个赞
Deer
2021 年10 月 15 日 14:21
2
这个网址在我收藏夹里躺了好多年。密歇根理工的在线讲义。
Sam
2021 年10 月 19 日 01:45
4
这两个我都看了。
中文的建议看《计算机辅助几何设计与非均匀有理B样条》 (CAGD&NURBS),施法中 编著的那本。啃完你会发现有很多新发现。
Sam
2021 年10 月 19 日 01:48
5
几本书都看完,用Rhino的时候,就发现Rhino里面的节点向量不对(在GH里面是可以全部显示曲面或者曲线的节点向量),但是也不知道为什么一直没修正。Rhino里面的节点向量在端头处少了一个。
Sam
2021 年10 月 19 日 01:51
6
对网页做笔记,可以使用【印象笔记】,或者【为知笔记】之类的软件,把整个网页收到自己的笔记里面,可以完整的保留内容,然后可以自己“翻译”,笔记、评论、修正,甚至可以分享给别人看。
Jorin
2021 年10 月 19 日 12:33
7
你所谓的“开源内核”指什么?Rhino 的内核 OpenNURBS 是开源的,但 这个 OpenNURBS 内核也是 McNeel 自己开发的,确实开发的时候有参考他人的书籍,分别是:
Bohm, Wolfgang, Gerald Farin, Jurgen Kahman (1984). A survey of curve and surface methods in CAGD , Computer Aided Geometric Design Vol 1. 1-60
DeBoor, Carl. (1978). A Practical Guide To Splines , Springer Verlag; ISBN: 0387953663
Farin, Gerald. (1997). Curves and Surfaces for Computer-Aided Geometric Design: A Practical Guide , 4th edition, Academic Press; ISBN: 0122490541
这里 讲的很清楚。
Sam
2021 年10 月 19 日 13:08
8
要是真的看了 De Boor的书,应该不会弄错节点向量的。
Jorin
2021 年10 月 19 日 13:08
9
Sam:
Rhino里面的节点向量不对
关于 Rhino 中 NURBS 曲线端点处节点向量数量的问题 ,这里 也讲的很清楚,怎么会少一个呢?另外, GH 调用的都是 RhinoCommon 的 API 开发的,怎么可能 GH 中是对的 Rhino 中不对?
https://developer.rhino3d.com/guides/rhinopython/primer-101/8-geometry/#87-nurbs-curves
我个人感觉Rhino应该不会犯这么低级的错误吧?
1 个赞
Sam
2021 年10 月 19 日 13:40
11
从CS3621的内容也可以得到这个公式:
Jorin
2021 年10 月 19 日 14:01
13
你这种算法是老的 NURBS 算法,但有的软件用的还是你写的这种算法,所以 Rhino 导出的时候会自动加两个点。
关于这一点, Rhino 有专门的说明,请看这里 :
https://wiki.mcneel.com/rhino/nurbsdoc
Rhino 玩的就是 NURBS ,在这个层面不会有这种低级错误的。
1 个赞
请教下,你这次和上次回复中截图的这些说明是哪个资料上的?我也想去看看。
Jorin
2021 年10 月 19 日 14:09
15
我把链接内置到文字里了,可能你没看到,我调整到外面了。
Jorin
2021 年10 月 19 日 14:15
17
另外,关于 Rhino 里几何的曲线、曲面、参考平面、网格等等,下面这个章节值得一读:
8 Geometry with Python (rhino3d.com)
Sam
2021 年10 月 19 日 15:29
19
没听说过NURBS有新的算法,Rhino这种应该是一种省略的“表示法”,所以不通用,在导入和导出的时候会在端点处自动删除和增加一个节点向量。
NURBS是完备体系,不是从代码层面说的,是在理论算法层面。
NURBS是增加了权重的B-Spline,去掉权重考虑B-spline即可。
节点向量的重复性,Knot vector multiplicity是不能乱的,在数学定义上,节点向量的重复个数是会影响B-spline的形状的。
Jorin
2021 年10 月 20 日 03:08
20
NURBS 本来就是用来表示曲线和曲面的,不用来表示曲线曲面,NURBS 存在的意义是什么呢?只是为了写几个公式或者让你多解几个方程?
你怎么理解不重要,重要的是并不如你所说 Rhino 的节点向量就是错误的:
也并不如你所说,开发 Rhino 的人没有像你一样看过 De Boor 的书,所以把节点向量弄错了:
更重要的是,Rhino 的内核 OpenNURBS 是开源的,大家都可以提交自己的更改 request,你如果坚持认为 OpenNURBS 中的节点向量是错的,你可以在 Github 中提交你的代码,或者 Fork 到你自己的仓库,更改出你认为正确的版本,甚至开发出自己的商业软件都是可以的:
https://github.com/mcneel/opennurbs
并且 OpenNURBS 的开源协议非常宽松,鼓励大家将 OpenNURBS 用于商业用途,而且并不会收取任何费用。
Sam
2021 年10 月 20 日 03:20
21
Rhino的开发者肯定是看过书的,但是这部分可能真的是一个没留意的错误,节点向量是一个一个隐藏的(隐藏几个的结果是不一样的),从Floating B-spline逐渐变成 Clamped B-spline,然后变成Periodic B-spline。
我现在并没有完全编写代码的能力,不过慢慢学吧,以后可能会做点东西。
其实你们能写代码的,可以试着从完全均匀的节点向量的B-spline(也就是Floating B-spline)开始,增加端点处的重复节点向量,能看到变化的。


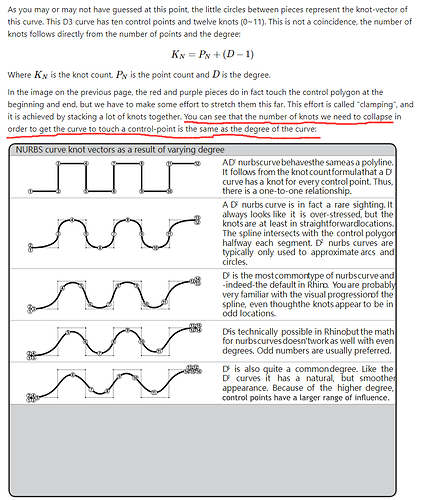
 不过我个人感觉NURBS中涉及的数学相对来说还是比较简单明了的(个人感觉和rudin那种数学分析比起来,NURBS的书简直太易读了),所以会否是表示习惯或者名称的误会?
不过我个人感觉NURBS中涉及的数学相对来说还是比较简单明了的(个人感觉和rudin那种数学分析比起来,NURBS的书简直太易读了),所以会否是表示习惯或者名称的误会?

